Algèbre linéaire : applications linéaires
Objectifs
Guide
Définitions
Définition d'une application linéaire
Définition. Soient
et
deux espaces vectoriels sur le même corps K. Une application
est une application linéaire si :
- pour tous et dans , ;
- pour tous
dans
et
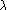 dans K, :
.
dans K, :
.
Cas particuliers.
Soit
une application linéaire.
- Si est le corps , on dit que est une forme linéaire sur .
- Si , on dit que est un endomorphisme de .
- Si est bijective, on dit que est un isomorphisme de dans (ou sur) .
- Si est bijective et , on dit que est un automorphisme de .
On note l'ensemble de toutes les applications linéaires de dans . Si , on note .
Propriétés
Proposition Soient
et
deux espaces vectoriels sur le corps
et
f une
application linéaire. Alors :
-
et pour tout
 ,
.
,
.
- Pour tous
dans
et
dans
, on a :
.
- Si est un sous-espace vectoriel de , alors est un sous-espace vectoriel de .
Proposition(définition
équivalente d'application linéaire) Soient
et
deux espaces
vectoriels sur le corps
. Une application
est une application linéaire si et seulement si
pour tous
et
dans
et 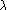
 ,
.
,
.
Exercice :
Image d'un vecteur par une application linéaire
Exemples
- Pour tout
-ev
, les applications
et
de
dans
définies pour
 par :
par :
et
sont des applications linéaires de dans , donc des endomorphismes de . On appelle l'application identique ou identité de , est un automorphisme de . On appelle l'application nulle de (malgré la notation, ne pas confondre avec l'élément neutre de ), n'est pas un automorphisme de . - L'application , , est une forme linéaire sur .
- L'application , est un endomorphisme de .
- L'application , , est un automorphisme de .
-
Soit
 . L'application
. L'application
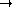 , :
, est une application linéaire.
, :
, est une application linéaire.
-
L'application
, où
(droite vectorielle de
engendrée par le vecteur
), définie pour
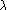

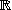 par
par
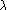 est un isomorphisme du
est un isomorphisme du 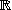 -ev
-ev
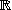 de dimension un sur le sev
de dimension un du
de dimension un sur le sev
de dimension un du 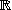 -ev
.
-ev
.
Identification
Les isomorphismes nous permettront d'identifier deux espaces vectoriels. Ainsi, on ne peut pas dire que la droite engendré par le vecteur (géométriquement, la première bissectrice du plan ) "est"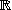 :
n'est pas un ensemble de nombres,
mais un ensemble de couples. Par contre, "
est isomorphe à
:
n'est pas un ensemble de nombres,
mais un ensemble de couples. Par contre, "
est isomorphe à 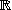 " est le langage
qui traduit le fait que, abstraction faite de la nature des éléments de
" est le langage
qui traduit le fait que, abstraction faite de la nature des éléments de
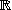 et de
,
ces deux espaces vectoriels ont les mêmes propriétés ou le même "comportement".
et de
,
ces deux espaces vectoriels ont les mêmes propriétés ou le même "comportement".
C'est bien une identification, pas une égalité : on aurait aussi pu considérer la droite comme engendrée par le vecteur et l'isomorphisme de
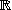 dans
(c'est-à-dire l'identification de
dans
(c'est-à-dire l'identification de 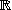 avec
)
aurait alors été l'isomorphisme
avec
)
aurait alors été l'isomorphisme
et donc un autre isomorphisme.
Noyau et image
- Noyau et image
- Injectivité, surjectivité
- Bases et propriétés d'une application linéaire
- Exemple
- Exercices
Noyau et image
Proposition et définition :
Soient
et
deux espaces vectoriels sur le corps
et
une application linéaire.
- L'ensemble = est un sous-espace vectoriel de , appelé le noyau de .
- L'ensemble est un sous-espace vectoriel de , appelé l'image de .
Exercice :
Image réciproque par une application linéaire
Injectivité, surjectivité
Proposition : Soient
et
deux espaces vectoriels sur le corps
et
une application
linéaire.
- est injective si et seulement si = .
- est surjective si et seulement si .
- est un isomorphisme si et seulement si et .
Proposition et définition :
Soient
et
deux espaces vectoriels sur le corps
et
une application linéaire. On suppose que
est de dimension finie
et que
est une base de
. Alors
est une suite génératrice
de
. Par conséquent le sous-espace
est de dimension
finie. On appelle rang de
, et on note
, la dimension de
.
Bases et propriétés d'une application linéaire
Lorsque l'espace vectoriel de départ d'une application linéaire est de dimension finie, l'on peut "tester" des propriétés de d'après l'action de sur les vecteurs d'une base de , comme le précise la proposition suivante. Proposition : Soient
et
deux espaces vectoriels sur le corps
et
une
application linéaire. Supposons que
est de dimension finie
non nulle et que
est une base de
.
- est injective si et seulement si est une suite libre de .
- est surjective si et seulement si engendre .
- est un isomorphisme si et seulement si est une base de .
Exemple
Exemple : Soient

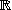 et
l'application linéaire
définie pour tout
par
. Soient
et
l'application linéaire
définie pour tout
par
. Soient

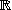 et
le plan vectoriel de
d'équation
. On veut déterminer, suivant les valeurs de
et
, le sous-espace vectoriel
de
.
Déterminons une base de
. Les vecteurs
et
sont deux vecteurs non colinéaires de
, donc
est une base de
. D'après la
proposition,
et
le plan vectoriel de
d'équation
. On veut déterminer, suivant les valeurs de
et
, le sous-espace vectoriel
de
.
Déterminons une base de
. Les vecteurs
et
sont deux vecteurs non colinéaires de
, donc
est une base de
. D'après la
proposition,

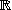 et
l'application linéaire
définie pour tout
par
. Soient
et
l'application linéaire
définie pour tout
par
. Soient

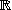 et
le plan vectoriel de
d'équation
. On veut déterminer, suivant les valeurs de
et
, le sous-espace vectoriel
de
.
Déterminons une base de
. Les vecteurs
et
sont deux vecteurs non colinéaires de
, donc
est une base de
. D'après la
proposition,
et
le plan vectoriel de
d'équation
. On veut déterminer, suivant les valeurs de
et
, le sous-espace vectoriel
de
.
Déterminons une base de
. Les vecteurs
et
sont deux vecteurs non colinéaires de
, donc
est une base de
. D'après la
proposition,
L'image d'une base par une application linéaire est une
suite génératrice de l'image de l'application linéaire.
est une suite génératrice de
.
Il y a plusieurs cas :
- soit
est non nul
L'application linéaire transforme une base de en une base de (car la matrice dont les colonnes sont les vecteurs , et est une matrice triangulaire, dont les coefficients diagonaux sont non nuls), d'après la proposition,Si est une base, est un isomorphisme si et seulement si est une base de .est un automorphisme de et la restriction de à est un isomorphisme de sur : alors est une base de et est un plan vectoriel de , pour tout

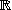 .
.
-
soit
est nul
L'application linéaire n'est plus un automorphisme de , mais on ne sait pas a priori si la restriction de à est un isomorphisme de sur . Calculons et ;
Exercices
Exercices : ces deux
exercices utilisent la matrice associée à une application linéaire.
- Base de l'image
- Base du noyau
Exercice :
Image et noyau
Exercice :
Image et noyau : application linéaire dépendant d'un paramètre
Matrices
- Matrice et application linéaire
- Exemple générique
- Exemple numérique
- Notation matricielle et systèmes linéaires
- Matrices et composition : le problème
- Produit de matrices
- Exercices sur le produit de matrices
- Matrices et composition : théorème
Matrice et application linéaire
Soient et deux espaces de dimension finie. La présence de bases dans et va nous permettre d'associer à toute application linéaire de dans une matrice.Définition Soient
et
deux espaces vectoriels de dimension finie
 et
et
 , respectivement. Soit
une application linéaire. Choisissons une base
de
et
une base
de
.
On appelle matrice de
dans les bases
et
la matrice
, notée
(ou parfois
),
dont la
-ième colonne est constituée par les coordonnées du vecteur
dans la base
, 1
, respectivement. Soit
une application linéaire. Choisissons une base
de
et
une base
de
.
On appelle matrice de
dans les bases
et
la matrice
, notée
(ou parfois
),
dont la
-ième colonne est constituée par les coordonnées du vecteur
dans la base
, 1 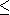
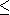 .
.
Lorsque
et
, on note
.
La matrice
est une matrice carrée d'ordre
.
Si on a, pour
:
 et
et
 , respectivement. Soit
une application linéaire. Choisissons une base
de
et
une base
de
.
On appelle matrice de
dans les bases
et
la matrice
, notée
(ou parfois
),
dont la
-ième colonne est constituée par les coordonnées du vecteur
dans la base
, 1
, respectivement. Soit
une application linéaire. Choisissons une base
de
et
une base
de
.
On appelle matrice de
dans les bases
et
la matrice
, notée
(ou parfois
),
dont la
-ième colonne est constituée par les coordonnées du vecteur
dans la base
, 1 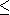
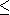 .
.
,
c'est-à-dire, si
sont les coordonnées du vecteur
dans la base
, alors :
Exemple générique
Prenons et . Si on aExemple numérique
Prenons et . Si on a
+
+
+
+
la matrice de
dans les bases
et
est +
+
+
.
C'est une matrice ayant 2 lignes et 4 colonnes.Exercice :
Matrice associée à une application linéaire
Notation matricielle et systèmes linéaires
Pour tous et
et
 ,
on note
et
les matrices colonnes des
coordonnées des vecteurs
dans la base
et
dans la base
, respectivement. Si
, on a alors :
,
on note
et
les matrices colonnes des
coordonnées des vecteurs
dans la base
et
dans la base
, respectivement. Si
, on a alors :
Autrement dit, si est la matrice de l'application linéaire dans les bases de et de :
résoudre l'équation
(où
 est donné et
est donné et
 est l'inconnue)
est l'inconnue) |
équivaut | résoudre le système linéaire | |
| déterminer le noyau Ker | équivaut | résoudre le système linéaire homogène ; | on obtient alors une base de Ker , un système d'équations paramétriques de Ker et un système d'équations cartésiennes de Ker |
| déterminer le rang de , une base et un système d'équations paramétriques de Im | équivaut | déterminer le rang de la matrice | c'est-à-dire le rang de la suite des vecteurs colonnes de |
| déterminer un système d'équations cartésiennes de Im | équivaut | chercher les conditions de compatibilité du système linéaire |
Matrices et composition : le problème
Question : Soient , et trois -espaces vectoriels de dimensions finies, munis des bases , et , respectivement. Soient , , . Peut-on calculer à partir de et ? Autrement dit, y a-t-il une opération sur des matrices qui correspond à la composition des applications linéaires qu'elles représentent ?Exemple : Soient
et
dont les matrices,
par rapport aux bases canoniques
de
et
de
sont, respectivement :
Peut-on calculer la matrice à partir des matrices et ?
Produit de matrices
Définition Soient
et
.
On appelle produit de la matrice
par la matrice
, et on note
, la matrice
définie par :
Le produit
n'est défini que si le nombre de colonnes de
est égal
au nombre de lignes de
. Le produit de deux matrices carrées de même ordre est toujours défini.
Exemple :
Exercices sur le produit de matrices
Exercice :
Trouver deux matrices dont le produit est donné II
Exercice :
Trouver deux matrices dont le produit est donné II
Matrices et composition : théorème
Proposition : Soient
,
et
trois espaces vectoriels sur le corps
,
de dimension finie
et
, munis des bases
,
et
respectivement. Si
 et
et
 ,
alors :
,
alors :
 et
et
 ,
alors :
,
alors :
La situation peut être visualisée :
Corollaire : Soient
des entiers strictement positifs. Si
,
et
sont dans
,
,
et
sont dans
,
et
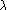
 , on a :
, on a :
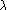
 , on a :
, on a :
- .
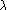 .
.
- .
- .
Corollaire : Soit
. L'ensemble
, muni de l'addition et du
produit de matrices :
est un anneau (non commutatif en général), dont l'élément unité est la matrice identité d'ordre , notée .
) et
est un anneau (non commutatif en général), dont l'élément unité est la matrice identité d'ordre , notée .
Prolongement par linéarité
Prolongement par linéarité
Comment "fabriquer" des applications linéaires ? Y a-t-il "peu" ou "beaucoup" d'applications linéaires entre deux -espaces vectoriels ? Nous allons y répondre quand l'espace de départ est de dimension finie. Théorème : Soient
et
deux espaces vectoriels sur le corps
. Supposons que
est de dimension finie
. Soient
une base de
et
une suite quelconque de vecteurs de
. Alors il existe une et une
seule application linéaire
telle que :
, 1 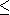
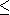
Corollaire : Soient
et
deux
-espaces vectoriels. Supposons que
est de dimension finie et qu'il existe un isomorphisme de
sur
. Alors
est de dimension finie,
et
il existe un isomorphisme de
dans
.
Définition :
Deux K-espaces vectoriels
et
sont dits
isomorphes s'il existe un isomorphisme de
sur
.
C'est le corollaire qui justifie cette définition, lorsque est de dimension finie ; lorsque ce n'est pas le cas, nous verrons un peu plus tard que l'application réciproque d'un isomorphisme est toujours un isomorphisme.
Corollaire : Soient
et
deux espaces vectoriels de dimension finie
et
 , respectivement. Soit
une application linéaire.
Choisissons une base
) de
et une base
de
.
L'application
M
(K) qui
à toute application linéaire
, respectivement. Soit
une application linéaire.
Choisissons une base
) de
et une base
de
.
L'application
M
(K) qui
à toute application linéaire
 fait correspondre
la matrice
de
dans les bases
et
est une application bijective.
fait correspondre
la matrice
de
dans les bases
et
est une application bijective.
 , respectivement. Soit
une application linéaire.
Choisissons une base
) de
et une base
de
.
L'application
M
(K) qui
à toute application linéaire
, respectivement. Soit
une application linéaire.
Choisissons une base
) de
et une base
de
.
L'application
M
(K) qui
à toute application linéaire
 fait correspondre
la matrice
de
dans les bases
et
est une application bijective.
fait correspondre
la matrice
de
dans les bases
et
est une application bijective.
Exemple de prolongement
Exemple : Soient
et
deux vecteurs de
.
Existe-t-il un et un seul endomorphisme
de
tel que
et
 ? Si oui, calculer
, pour
.
? Si oui, calculer
, pour
.
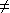 -2.
-2.
 ? Si oui, calculer
, pour
.
? Si oui, calculer
, pour
.
-
Si est différent de -2,
est une base de et le théorème de prolongement assure l'existence et l'unicité de l'endomorphisme vérifiant les conditions données. Soit , pour calculer il suffit d'exprimer dans la base et utiliser la linéarité de : , d'où :
= .
-
Si a = -2,
alors v= -2u ; s'il existe un endomorphisme f de vérifiant les conditions données, on a forcément f(v)= -2f(u) ; par conséquent, si , il n'existe pas de tel endomorphisme ; si b =4, il existe une infinité d'endomorphismes f de tels que f(u)=(-2,3) et : soit un vecteur non colinéaire à u, c'est-à-dire, tel que ; (u,w) est une base de et donc, par le théorème de prolongement pour tout , il existe un endomorphisme (unique) de tel que f(u)=(-2,3) et f((a,b))=(c,d).
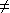 -2.
-2.
Exercice sur le prolongement
Exercice
Existence d'une application linéaire
Le théorème du rang
Théorème du rang
Un théorème important dont la démonstration utilise la notion de supplémentaire est le théorème du rang. Théorème :
Soient
E et
F deux K-espaces vectoriels, avec
E de dimension finie et
f une application linéaire. Alors
Im f est un sous-espace vectoriel de
F de dimension finie et on a :
dim E = dim Ker f + rang f
Corollaire fondamental : Soient
E et
F deux K-espaces vectoriels de même dimension finie
n et
f une application linéaire. Les conditions suivantes sont équivalentes :
- f est un isomorphisme de E sur F.
- f est injective.
- f est surjective.
Exemple d'application du théorème du rang
Application. Le TNI
permet de résoudre certains exercices avec peu de calculs.
Par exemple, soit
l'application linéaire dont la matrice, par rapports aux bases canoniques
de
et
, est
Allons-y.
.
Déterminons Ker f.Allons-y.
La matrice
A, donc
f, a rang 2. D'après le TNI,
dim Ker f = 3 - 2 = 1, donc Ker
f est une droite vectorielle de
. Notons
(e1 , e2 , e3) la base canonique de
,
on "voit" que
,
d'où
est un vecteur non nul de Ker
f, qui est
de dimension 1, donc
u est une base de Ker
f et
.
Changement de bases
- Matrice de changement de bases : définition
- Matrice de changement de bases : propriétés
- Changements de base sur les vecteurs
- Changement de bases sur les matrices
- Exercices sur le changement de base
Matrice de changement de bases : propriétés
Si iE est l'application identique, on a e'j=iE(e'j), , donc P est la matrice de l'application iE dans les bases de E (en tant qu'espace de départ) et de E (en tant qu'espace d'arrivée). Cette interprétation de P est fort importante dans la plupart des raisonnements sur les matrices de changement de base :.
Remarque :
On a
,
la matrice identité d'ordre
n. La matrice
P
est la matrice de
iE lorsqu'on considère dans l'espace de départ
"la nouvelle base"
et dans l'espace d'arrivée "l'ancienne base"
. Donc,
P est la matrice des "nouveaux vecteurs"de base,
par rapport aux "anciens" vecteurs de base.
Proposition : Soient
E un
K-espace vectoriel de dimension finie
,
et
deux bases de
E. La matrice
P  Mn(K)
de passage de la base
à la base
est inversible et
est la matrice de passage de la base
à la base
.
Mn(K)
de passage de la base
à la base
est inversible et
est la matrice de passage de la base
à la base
.
 Mn(K)
de passage de la base
à la base
est inversible et
est la matrice de passage de la base
à la base
.
Mn(K)
de passage de la base
à la base
est inversible et
est la matrice de passage de la base
à la base
.
Changements de base sur les vecteurs
Proposition : Soient
E un
K-espace vectoriel de dimension finie
,
et
deux bases de
E et
x  E. Notons
X et
X' les matrices colonnes des coordonnées du vecteur
x dans les bases
et
, respectivement. Alors :
E. Notons
X et
X' les matrices colonnes des coordonnées du vecteur
x dans les bases
et
, respectivement. Alors :
 E. Notons
X et
X' les matrices colonnes des coordonnées du vecteur
x dans les bases
et
, respectivement. Alors :
E. Notons
X et
X' les matrices colonnes des coordonnées du vecteur
x dans les bases
et
, respectivement. Alors :
X = P X' et X' = P-1 X
Exercice :
Changement de bases sur les vecteurs
Changement de bases sur les matrices
Proposition :
Soient
E et
F deux espaces vectoriels de dimensions finies
n et
p, respectivement. Soient
et
deux bases de
E,
et
deux bases de
F,
P  Mn(K) (resp.
Q
Mn(K) (resp.
Q  Mp(K))
la matrice de passage de passage de la base
à la base
(resp. de la base
à la base
).
Soient
f
Mp(K))
la matrice de passage de passage de la base
à la base
(resp. de la base
à la base
).
Soient
f  L(E,F),
et
. Alors :
L(E,F),
et
. Alors :
 Mn(K) (resp.
Q
Mn(K) (resp.
Q  Mp(K))
la matrice de passage de passage de la base
à la base
(resp. de la base
à la base
).
Soient
f
Mp(K))
la matrice de passage de passage de la base
à la base
(resp. de la base
à la base
).
Soient
f  L(E,F),
et
. Alors :
L(E,F),
et
. Alors :
A' = Q-1 A P
Corollaire.
Soient
E un
K-espace vectoriel de dimension finie
n,
et
deux bases de
E. Soient
f  L(E,F),
et
. Soit
P
L(E,F),
et
. Soit
P  Mn(K)
la matrice de passage de passage de la base
à la base
. Alors :
Mn(K)
la matrice de passage de passage de la base
à la base
. Alors :
 L(E,F),
et
. Soit
P
L(E,F),
et
. Soit
P  Mn(K)
la matrice de passage de passage de la base
à la base
. Alors :
Mn(K)
la matrice de passage de passage de la base
à la base
. Alors :
A' = P-1 A P
Exercices sur le changement de base
Exercices :
- Changement de bases
- Matrice d'une application linéaire dans différentes bases
- Changement de base théorique
Matrice de changement de bases : définition
Questions Soient
E et
F deux
K-espaces vectoriels de dimension finie, munis des bases
et
,
respectivement. Comment changent les coordonnées d'un vecteur de
E lorsqu'on change de base dans
E ? Comment change la matrice de
f  L(E,F) lorsqu'on change de base dans
E et
dans
F ?
Nous allons voir que les changements de base s'expriment par des produits de matrices.
L(E,F) lorsqu'on change de base dans
E et
dans
F ?
Nous allons voir que les changements de base s'expriment par des produits de matrices.
 L(E,F) lorsqu'on change de base dans
E et
dans
F ?
Nous allons voir que les changements de base s'expriment par des produits de matrices.
L(E,F) lorsqu'on change de base dans
E et
dans
F ?
Nous allons voir que les changements de base s'expriment par des produits de matrices.
Définition :
Soient
E un
K-espace vectoriel de dimension finie
,
= (u1, u2, ... , un) et
deux bases de
E. La matrice
dont la j-ième colonne est constituée par les coordonnées du vecteur u'j dans la base , , est appelée la matrice de passage de la base à la base . Si on a, pour :
u'j = pj u1 + p2j u2 + ... + pn j un,
c'est-à-dire, si , p2j, ..., pn j sont les coordonnées du vecteur u'j dans la base , alors :