OEF Intégrale définie
--- Introduction ---
Ce module regroupe pour l'instant 21 exercices sur les intégrales définies d'une
variable (théorie et calcul).
Il y a d'autres modules d'exercices sur les applications d'intégrales
définies :
OEF intégrale géométrique pour les applications en géométrie, et
OEF intégrale physique pour les applications en physique.
Changement de bornes I
Soit
une fonction telle que
.
Calculer la fonction
définie par
.
Changement de bornes Ib
Soit
une fonction telle que
. Calculer la fonction
définie par
.
Changement de bornes II
Soit
une fonction telle que
. Calculer la fonction
définie par
.
Changevar I
Soit
une fonction continue. Pour faire un changement de variable d'une intégrale définie comme suit, quelles valeurs de
et
faut-il prendre ?
Changevar II
Soit
une fonction continue. Pour faire un changement de variable d'une intégrale définie comme suit, quelles valeurs de
et
faut-il prendre ?
Fonction & dérivée I
Soit une fonction dérivable
vérifiant
et
. Que vaut
? Votre réponse doit avoir une précision d'au moins 1/10000.
Fonction & dérivée II
Soit une fonction dérivable
telle que
et
. Que vaut
? Votre réponse doit avoir une précision d'au moins 1/10000.
Fonction & dérivée III
Soit une fonction dérivable
avec
, où
est une constante. Sachant que
et
,
quelle est la valeur de
? Votre réponse doit avoir une précision d'au moins 1/10000.
Intégrale numérique
Calculer l'intégrale
à une précision de 0.01 %.
Inverse polynome
XXXXX La fonction
définie par
est continue et strictement monotone sur l'intervalle
(vérifiez), avec
,
. Donc elle a une fonction réciproque
définie sur l'intervalle
. Calculez l'intégrale
Indication. Pour une fonction continue bijective
, on a
.
.
Limdef intégrale I
Calculez la limite suivante en utilisant la définition d'intégrale définie:
.
Limdef intégrale II
Calculez la limite suivante en utilisant la définition d'intégrale définie:
.
Limdef intégrale III
Calculez la limite suivante en utilisant la définition d'intégrale définie :
Moyenne de fonction
Calculez la moyenne de la fonction
définie par
sur l'intervalle [,].
Changement de variable avec du sin
On souhaite trouver
,
(avec
) et la fonction
tels que
=
avec le changement de variable
.
puis calculer la valeur de l'intégrale. Si
choisir
et
dans [-pi/2,pi/2]
et
L'intégrale vaut
Pour entrer la réponse, on utilise les conventions suivantes :
La fonction logarithme népérien s'écrit log. Par exemple, on tape log(2) pour écrire le réel ln(2).
La fonction racine carrée s'écrit sqrt. Par exemple, on tape sqrt(2) pour écrire le réel
.
Mettez * pour les multiplications.
Écrire pi pour
.
Intégrales définies et aires 1
Calculer
.
On a
. Voici la représentation graphique de la fonction
xrange -2, yrange , hline 0,0,black vline 0,0,black segment 0,,1,,yellow trange 0, plot black,t, trange -2, segment 1,,1,,black dsegment 1,,1,,black segment 0,,0,,black text black,-0.2,-0.2,medium,0 text black,0.6,-0.2,medium,1 gridfill ,*4/5,5,5, gridfill /2,*4/5,5,5, transparent yellow
Compléter l'affirmation suivante :
L'aire de la zone hachurée en représente
de
lorsque
tend vers
L'aire de la zone hachurée en représente
de
lorsque
tend vers
Calculer les limites de
lorsque
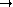
+

et lorsque
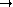
0.
Consigne : écrire
inf pour +

et
-inf pour -

; écrire
non si la limite n'existe pas.
Intégrales définies et aires 2
Soit
.
Calculer
.
=
On a
. Le graphe de la fonction
définie par
est le suivant :
xrange -0.2,4*pi yrange -*5/4,*5/4 hline 0,0,black vline 0,0,black plot black, gridfill pi/2,*4/5,10,10,blue gridfill 3*pi/2,*4/5,10,10,blue gridfill 5*pi/2,*4/5,10,10,blue gridfill 7*pi/2,*4/5,10,10,blue
Calculer
.
=
Consigne : si la limite n'existe pas, répondre non; si elle est infinie, répondre inf.
Intégrale avec sin cos
En faisant le changement de variable
, déterminer la fonction
telle que
.
.
L'intégrale vaut
.
Donner les valeurs exactes et mettre * pour la multiplication.
Positive-Négative II
Soient deux fonctions continues
et
, définies sur l'intervalle [0,1], telles que
. Parmi les propriétés suivantes, repérez celle dont vous êtes certain qu'elle est
.
Positive-Négative
Soit une fonction continue
définie sur l'intervalle [0,1], telle que
. Parmi les propriétés suivantes, repérez celle dont vous êtes certain qu'elle est
.
Somme de Riemann
Calculez la limite suivante en utilisant la définition d'intégrale définie :
Pour entrer la réponse, on utilise les conventions suivantes :
La fonction logarithme népérien s'écrit log. Par exemple, on tape log(2) pour écrire le réel ln(2).
La fonction arctangente s'écrit atan. Par exemple, on entre atan(2) pour écrire le réel
.
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur les intégrales définies à une variable (théorie et calcul). interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, analysis, integral, definite_integral,area
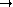 +
+ et lorsque
et lorsque
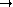 0.
0.  et -inf pour -
et -inf pour -  ; écrire non si la limite n'existe pas.
; écrire non si la limite n'existe pas.