Gradient
Objectifs
- Mettre l'accent sur différentes manières de représenter graphiquement les fonctions de deux variables
- Considérer les dérivées partielles des fonctions de plusieurs variables du point de vue plus géométrique du gradient.
- Insister sur l'aspect "approximation linéaire" de la différentielle.
Documents
J. Stewart, Analyse, concepts et contextes, vol. 2, DeBoeck Université (2001)
Guide
Exemples concrets de fonctions de plusieurs variables
Dans la vie, ce sont les fonctions d'une variable qui sont rares et les fonctions de plusieurs variables fréquentes ! Pour se faciliter la vie, celui qui modélise prétend que certaines sont des paramètres et d'autres des variables. Ce qui "signifie" qu'il va faire comme si certaines des variables étaient constantes.Donnons quelques exemples :
Exemples :
On parle en physique de champ scalaire :
scalaire vient du fait que l'image est contenue dans les scalaires
- la température, la pression comme fonction de la position sur une carte : fonction de deux variables et
- l'altitude en un point d'une carte : fonction de deux variables et
- la température, la pression en chaque point d'une pièce (en trois dimensions) : fonction de trois variables , et
- le volume d'une boîte en fonction de la hauteur, de la largeur et de la profondeur : fonction de trois variables et et .
-
votre moyenne sur WIMS en fonction du temps et de la feuille d'exercice :
fonction de deux variables
et
(mais ici heureusement la variable
est une variable dite discrète (un entier) et pas continue (dans
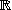 )
)
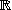 , champ vient de ce que le domaine de définition est dans
.
, champ vient de ce que le domaine de définition est dans
.
Exercices :
Champ scalaire
Dérivées partielles
Exercices de calcul de dérivées partielles
On notera les dérivées partielles d'une fonction d'une des manières suivantes : Si est une fonction de deux variables (x,y), la dérivée partielle de par rapport à est notée indiféremment
,
,
Avant de commencer, il faut savoir calculer des dérivées partielles,
nous proposons donc d'abord ici des exercices de technique.
Exercices :
- Calcul de dérivées partielles
- Calcul de dérivées partielles secondes
- Dérivées partielles de composés de fonctions
- Dérivées partielles secondes de composés de fonctions
Gradient
Définition du gradient
Soit
une fonction de 3 variables. On lui
associe un champ de vecteurs appelé champ de gradient
et noté grad
ou 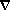 :
:
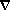 :
:En posant ,
grad
.
Exercice
Autres notations :
- en utilisant la base canonique (
e1,
e2,
e3
)
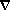 f =
f =
-
En physique, on utilise la notation suivante :
,
,
ce qui donne les formules suivantes
dansou en mettant les scalaires après les vecteurs contrairement à nos habitudes
dansdans
dans .
Dérivée directionnelle
Soit un vecteur de et un point de : on a alors Soit
un vecteur unitaire de
. On appelle
dérivée directionnelle de
dans la direction
au point
(ou encore la
dérivée partielle de
dans la direction
au point
) le nombre
Si la direction est donnée par un vecteur qui n'est pas unitaire, il faut
le rendre unitaire en le divisant par sa norme :
.
.
Propriété :
La dérivée directionnelle est
de norme maximale dans la
direction du gradient et la direction dans laquelle la fonction
croît le plus vite
est la direction du gradient.
Démonstration
Si
et
sont deux vecteurs d'angle
, on a l'égalité
Ainsi,
et l'égalité a lieu si et seulement si les vecteurs
et
sont colinéaires.
En particulier, si
est un vecteur unitaire,
et
est égal à
(et donc maximal) si
est colinéaire au gradient de
en
.
Exercices
Exercice :
Dérivées directionnelles
Exercice :
Gradient et croissance de la fonction
Approximation
- Approximation linéaire
- Differentiabilité
- Estimation d'erreurs
- Quelques exemples tirés de la physique
- Approximation numérique
- Gravitation et approximation
- Exercice : Approximation linéaire
Approximation linéaire
Définition :
Soit
une fonction de deux variables
définie au voisinage d'un point
. On dit que la fonction affine
est une approximation linéaire ou plus exactement affine
de
au point
si l'on peut écrire
avec des fonctions
et
tendant vers 0
lorsque
.
De manière équivalente, on peut aussi dire que la limite de
tend vers 0 lorsque
.
On dit que l'on a linéarisé au voisinage de : pour certains problèmes, on "peut" remplacer par son approximation linéaire.
Lorsqu'on regarde la surface d'équation , si est l'approximation affine de en , l'équation définit un plan dans qui est le plan tangent à la surface en . Cela sera revu dans le chapitre sur les surfaces.
Exercice
Trouver l'approximation linéaire d'une fonction
Differentiabilité
Définition :
Soit
une fonction de 2 variables
définie au voisinage d'un point
. On dit que
est différentiable
si
admet une approximation linéaire.
Théorème : Si
est
une
fonction de classe
Autrement dit :
On dit qu'une fonction définie sur un ouvert de
est
de classe
si elle est continue et admet
des dérivées partielles premières continues.
dans un voisinage de
,
est différentiable et son approximation linéaire
est donnée par
 est une fonction de
définie au voisinage de
telle que
est une fonction de
définie au voisinage de
telle que
.
,
.
 est une fonction de
définie au voisinage de
telle que
est une fonction de
définie au voisinage de
telle que
.
 est une fonction de
définie au voisinage de
telle que
est une fonction de
définie au voisinage de
telle que
.
Estimation d'erreurs
On rencontre couramment en physique le problème suivant : On a une quantité , fonction connue des quantités ... Ayant fait des mesures des quantités avec une certaine incertitude, on se demande avec quelle incertitude est connue . Mathématiquement, on dispose des objets suivants- Une fonction
- Un point : , c'est le point qu'on mesure
- Un rectangle : par exemple les nombres et représentent les erreurs maximales de mesure.
- Un point : un point du rectangle, c'est le point que l'on est en train de mesurer, on ne le connaît donc pas très précisément
- L'approximation numérique au point :
- Les dérivées partielles de : , sur le rectangle , ou encore ce qui revient au même la différentielle de .
- La majoration de l'erreur : Elle est obtenue en
apppliquant le théorème suivant
:
Soit une fonction définie sur un rectangle de centré en , défini par , . Alors, si est un point de , on a la majoration suivante :avec un majorant de sur et un majorant de sur .
C'est une conséquence de la formule de Taylor à une variable appliquée à la fonction définie par
Quelques exemples tirés de la physique
Calculs d'erreur
Exemple :
La mesure du rayon d'un disque donne
cm.
Calculer la surface
du disque, ainsi que les incertitudes de la mesure
(erreur absolue et erreur relative).
Solution
Solution
Plaçons nous dans le cadre mathématique : il s'agit de trouver la fonction
qui est ici une fonction d'une variable
- La fonction définie par
- Le point :
- L' intervalle : par exemple
- Le point mesuré : un point de l'intervalle
- L'approximation numérique au point :
- La majoration de l'erreur : il
s'agit
Soit une fonction définie sur un intervalle dede majorer sur l'intervalle par exemple :
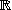 centré en
, défini par
.
Alors, si
est un point de
, on a la majoration suivante :
avec un majorant de sur .
centré en
, défini par
.
Alors, si
est un point de
, on a la majoration suivante :
avec un majorant de sur .
Calculs d'erreur
Exemple :
La mesure des côtés d'un rectangle donne
cm et
cm. Calculer la surface
du rectangle, ainsi
que les incertitudes de la mesure (erreur absolue et erreur relative).
Solution
Solution
Plaçons-nous dans le cadre mathématique : il s'agit de trouver la fonction, le rectangle ...
- La fonction : définie par
- Le point :
- Le rectangle : par exemple
- Le point mesuré : un point du rectangle, c'est le point que l'on est en train de mesurer
- L'approximation numérique au point :
-
La majoration de l'erreur : il
s'agit
Soit une fonction définie sur un rectangle de centré en , défini par , . Alors, si est un point de , on a la majoration suivante :de majorer sur le rectangle , par exemple :avec un majorant de sur et un majorant de sur .
Calcul d'erreurs
Exemple :
Un sac contient 3.3 kg
g de bonbons. Pour estimer
le nombre de bonbons présents dans le sac, on pèse un bonbon au hasard
et on obtient 20 g
g. On suppose que tous les bonbons
sont identiques. Calculer le nombre total de bonbons avec l'incertitude absolue et relative.
Solution
Solution
Plaçons-nous dans le cadre mathématique : il s'agit de trouver la fonction, le rectangle ...
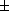 9.7 près et que l'erreur relative est de
qui est inférieure à
% .
9.7 près et que l'erreur relative est de
qui est inférieure à
% .
- La fonction : définie par
- Le point :
- Le rectangle : par exemple
- Le point mesuré : un point du rectangle, c'est le point que l'on est en train de mesurer.
- L'approximation numérique au point : .
- Les dérivées partielles de : , :
- La majoration de l'erreur : il
s'agit
Soit une fonction définie sur un rectangle de centré en , défini par , . Alors, si est un point de , on a la majoration suivante :de majorer sur le rectangle par exemple :avec un majorant de sur et un majorant de sur .
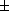 9.7 près et que l'erreur relative est de
qui est inférieure à
% .
9.7 près et que l'erreur relative est de
qui est inférieure à
% .
Calcul d'erreurs
Exemple :
L'indice d'un milieu transparent à la lumière est
.
Calculer l'incertitude relative commise sur
en fonction de
,
et des
incertitudes de mesures sur
et sur
pour
degrés,
degrés avec des incertitudes de mesure de 2 minutes d'angle.
Solution
Solution
Plaçons nous dans le cadre mathématique : il s'agit
de trouver la fonction, le rectangle et il ne faut pas oublier de convertir
les degrés et les minutes en radians.
- La fonction : définie par
- Le point :
- Le rectangle : par exemple .
- Le point mesuré : un point du rectangle, c'est le point que l'on est en train de mesurer.
- L'approximation numérique au point :
- Les dérivées partielles : ,
- La majoration de l'erreur : il
s'agit
Soit une fonction définie sur un rectangle de centré en , défini par , . Alors, si est un point de , on a la majoration suivante :de majorer sur le rectangle par exemple un majorant est (autour des points 1.151 et 0.628, la fonction sinus est croissante et la fonction cosinus est décroissante)avec un majorant de sur et un majorant de sur .
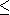 0.01
)
0.01
)
Calculs d'erreurs
Exemple :
Au minimum de déviation
, l'indice
d'un prisme d'angle au sommet
d'angle
est donné par
.
Calculer l'incertitude relative de l'indice en prenant
degrés,
degrés, incertitude sur
= 0.02 degrés, incertitude sur
= 0.14 degrés.
Solution
Solution
Plaçons-nous dans le cadre mathématique : il s'agit de trouver la fonction, le rectangle ...
- La fonction : définie par
- Le point : : les angles en degrés sont convertis en radians.
- Le rectangle : par exemple .
- Le point mesuré : un point du rectangle, c'est le point que l'on est en train de mesurer.
- L'approximation numérique au point :
-
Les dérivées partielles :
,
- La majoration de l'erreur : il
s'agit
Soit une fonction définie sur un rectangle de centré en , défini par , . Alors, si est un point de , on a la majoration suivante :de majorer sur le rectangle par exemple un majorant est (autour des points 1.047 et 0.401, la fonction sinus est croissante et la fonction cosinus est décroissante)avec un majorant de sur et un majorant de sur .
Approximation numérique
Supposons que l'on connaisse l'approximation linéaire de la fonction en . Pour calculer une approximation du nombre avec proche de , on peut utiliser cette approximation linéaire . Exemple :
L'approximation affine en
de la fonction définie par
est
.
Une approximation de
est donc
obtenue en évaluant
en
et
. La "vraie" valeur de
ou plutôt une meilleure approximation
est
.
Mais sans autre précision, on ne peut pas connaître
l'erreur commise, c'est-à-dire une majoration de la différence (en valeur abolue) entre
et
. Ce problème a déjà été rencontré dans
le
cas des fonctions d'une variable.
Dans ce cas là, cette erreur est majorée par
pour
un intervalle contenant
et
(application de la formule de Taylor-Lagrange),
Dans le cas de deux variables,
on utilise aussi une
formule de Taylor-Lagrange qui fait intervenir les dérivées partielles d'ordre 2.
Soit
une fonction de classe
sur une boule
(ou un rectangle)
de centre
.
Alors, si
est un point de B, il existe
tel que
+
Idée de la démonstration
La formule se montre à partir de la formule pour une
fonction à une variable
donnée par
On a alors
et
.
On en déduit que
Soit
une fonction
définie sur un rectangle
de
centré en
, défini par
,
.
Alors, si
est l'approximation linéaire de
au point
, on a la majoration
suivante et si
est un point de
:
avec
un majorant de
sur
,
un majorant
de
sur
,
un majorant de
sur
.
Exemples
Gravitation et approximation
Cet exemple concerne en fait une fonction d'une variable. Reprenons un énoncé de physique : Exercice :
A la surface de la terre, la norme du champ de gravitation
est
où
est la constante de gravitation,
la masse de la terre et
le rayon de la terre. A l'altitude
, on a
Si
, donner en fonction de
,
et
une expression approchée de
en utilisant un développement limité au second ordre en
(ou plutôt la formule de Taylor-Lagrange à l'ordre 2). Calculer l'erreur relative.
Une solution
Posons . On a
Le développement limité de
à l'ordre 2 est
Une expression approchée
de
est
Quelle erreur a-t-on fait ? Grossièrement, on peut dire qu'elle est de l'ordre de
.
Soyons précis. Montrons que si
et si
,
Preuve
Par la formule de Taylor-Lagrange (ou par l'inégalité de Taylor-Lagrange), on a l'inégalité
avec
. On calcule la dérivée troisième de
:
En revenant à notre problème initial, pour
Si l'on considère l'approximation satisfaisante lorsque l'erreur
relative est inférieure à 1.5%, l'altitude maximum admissible est
vérifiant
c'est-à-dire
km
avec le rayon de la terre
égal à 6380 km.
Une solution
Posons . On a
Par la formule de Taylor-Lagrange (ou par l'inégalité de Taylor-Lagrange), on a l'inégalité
,
Pour
, on a
et
En revenant à notre problème initial, pour
Exercice : Approximation linéaire
Exercice :
Trouver l'approximation linéaire d'une fonction
Courbes de niveau
- Courbes de niveau
- Exemples
- Courbes de niveau et surfaces
- Exercices
- Tangente aux courbes de niveau
- Tangente, normale et gradient
- Et lorsque le gradient est nul ?
- Gradient et courbes de niveau
Courbes de niveau
Définition :
Soit
une fonction définie sur un ouvert
de
. On appelle courbe de niveau de
associée au réel
l'ensemble des points (x,y) de
vérifiant
. Cet ensemble est éventuellement vide.
- L'exemple le plus naturel et qui a donné son nom aux courbes de niveau est celui des cartes topographiques. Si l'on voit comme l'altitude en un point , la courbe de niveau est bien ce qui est appelé courbe de niveau en géographie ou cartographie. Les courbes de niveau sont les courbes d'altitude constante. Les courbes de niveau sont tracées pour des altitudes régulièrement espacées par exemple tous les 100 m.
- Si représente la température en un point , c'est ce qu'on appelle courbe isothermale ou isotherme .
On dessine les courbes de niveau de pour des valeurs de de la forme , , , , ... On dit alors qu'elles sont équiréparties.
Un exemple :
Courbes de niveau de la fonction
définie par
pour
:
.
En utilisant l'outil
Tracé de la surface
, comparer le dessin en 3D avec le dessin des courbes de niveau.
Vous pouvez aussi une fois la fenêtre de tracé ouverte rajouter l'équation du plan horizontal
dont vous désirez voir la section avec la surface : z= ?D'autres exemples
D'autres exemples plus compliqués
Exemples
Exemple :
Courbes de niveau de la fonction
définie par
pour
:
.
En utilisant l'outil
Tracé de la surface
, comparer le dessin en 3D avec le dessin des courbes de niveau.
Vous pouvez aussi une fois la fenêtre de tracé ouverte rajouter l'équation du plan horizontal
dont vous désirez voir la section avec la surface : z= ? Courbes de niveau et surfaces
Courbes de niveau de la fonction
pour
:
.
En utilisant l'outil
Tracé de la surface
, comparer le dessin en 3D avec le dessin des courbes de niveau.
Vous pouvez aussi une fois la fenêtre de tracé ouverte rajouter l'équation du plan horizontal
dont vous désirez voir la section avec la surface : z= ? Exercices
Exercices :
Faire le lien entre représentation graphique d'une fonction de 2 variables
(c'est-à-dire la représentation de la surface
) et les courbes de niveau de
.
- Représentation graphique et courbes de niveau 1
- Représentation graphique et courbes de niveau 2
Dans les exercices suivants, la fonction
est une fonction des coordonnées polaires du plan
.
Cela arrive très naturellement. Par exemple, dans les problèmes de
, chimie atomistique,
On demande de faire le lien entre les courbes de niveau , représentées dans le plan et les fonctions et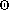 .
.
en fait, il s'agit alors de fonctions de trois variables exprimées en coordonnées sphériques
la fonction est même le produit d'une fonction de
par une fonction de
:
.
On demande de faire le lien entre les courbes de niveau , représentées dans le plan et les fonctions et
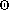 .
.
- Représentation graphique et courbes de niveau (polaires)
- Représentation graphique et courbes de niveau (polaires)
- Représentation graphique et courbes de niveau (polaires)
Exercice : Reconnaître une fonction
par sa représentation graphique :
- Représentation graphique et fonction, 1
- Représentation graphique et fonction, 2
- Représentation graphique et fonction, 3
Tangente aux courbes de niveau
Théorème :
Soit
une fonction
sur un ouvert
de
et
un point de
avec
.
On suppose que le gradient de
est non nul en
. La tangente en
à la courbe d'équation
a comme équation
Démonstration
grad
ou encore
Nous ne donnons ici qu'une idée de la démonstration
en supposant que localement la courbe d"équation
peut être paramétrée,
c'est-à-dire qu'il existe deux fonctions
et
d'un intervalle ouvert
contenant 0 dans
telles que
Prenons la valeur en
:
Le vecteur grad
est donc normal au vecteur
. Or ce vecteur est le vecteur dérivé de la courbe paramétrée
et appartient donc à la tangente à la courbe en
.
- pour
Exercice :
Vérifier que si
est la courbe d'équation
, on retrouve
l'équation usuelle de la tangente (prendre
).
Tangente, normale et gradient
Propriété :
Les courbes de niveau d'une fonction
sont perpendiculaires au gradient de
.
Démonstration
Démonstration
La droite
tangente
à la courbe d'équation
au point
avec
admet comme équation
grad
lorsque grad
;
autrement dit
`
et la tangente en
est perpendiculaire au vecteur grad
(c'est une
droite affine à propos).
Exercice :
Gradient, tangente et normale
Et lorsque le gradient est nul ?
Exemple :
Courbes de niveau de la fonction
définie par
pour
:
.
Lorsque
,
grad
est nul au point
et on ne peut donc pas définir de tangente à la courbe en ce point à l'aide du gradient.Que peut-on faire ? On peut quand même deviner qu'il y a des tangentes à la courbe.
Supposons qu'il existe une courbe paramétrée , définie sur un intervalle ouvert contenant 0 et telle que pour et . Cherchons ce que l'on peut dire du vecteur tangent à . En dérivant l'équation, on obtient
Dérivons-la de nouveau
Ici, on obtient
Pour mieux comprendre en appliquant :
,
,
et
Exercice sur
les courbes paramétrées et les équations implicites de courbes
Gradient et courbes de niveau
Les variations de la norme du gradient peuvent se deviner sur le dessin des courbes de niveau équidistribuées. Ainsi, sur une carte géographique, les endroits pentus sont ceux où les lignes de niveau sont très rapprochées. Exercice :
comparaison du gradient en deux points