Géométrie du plan
Géométrie du plan
Ce document est conçu comme une initiation à la géométrie du plan et une introduction à l'utilisation des groupes. Ce travail mène naturellement à l'étude des frises et des pavages, ce qui est abordé dans un autre document.
Il a été développé au fil d'un cours d'ouverture à l'intention d'étudiants de L1 et L2 comme une promenade dans la géométrie du plan.
IV Groupes et groupes d'isométrie
Document pdf
I De la géométrie aux groupes
Nous allons commencer par parler de quelques groupes simples.
I-1 Géométrie et géométrie
- La géométrie des triangles, de droites, des figures : Les grecs calculent avec la géométrie
(construire le nombre dont le carré est 5, trouver le pgcd de deux nombres).Euclide : Couper une droite donnée, de manière que le rectangle compris sous la droite entière et l'un des segments, soit égal au carré du segment restant.
SolutionCouper une droite donnée, de manière que le rectangle compris sous la droite entière et l'un des segments, soit égal au carré du segment restant.
Voir la construction
On prend un segment .
{proof}
= Or : donc et
{proof}Descartes : Soit l'unité et qu'il faille multiplier par , je n'ai qu'à joindre les points et , puis tirer parallèle à , et est le produit de cette multiplication.
Ou s'il faut tirer la racine carrée de , je lui ajoute en ligne droite , qui est l'unité, et en divisant en deux parties égales au point , du centre , je tire le cercle , puis élevant du point une ligne droite jusques à à angles droits sur ; c'est la racine cherchées
SolutionConstruire la racine carrée d'un nombre représenté par un segment.
Voici le segment de longueur . Ou s'il faut tirer la racine carrée de ,
- La géométrie analytique ou cartésienne : on repère un point par ses coordonnées
. Une
droite a une équation
, on donne des expressions analytiques pour les transformations.
Exemple
Trouver anaytiquement le point d'intersection de la droite passant par et et de la droite d'équation . - La géométrie devient algèbre : on s'intéresse aux structures,
aux transformations plutôt qu'aux objets et à leurs propriétés.
Ainsi les dessins sont les mêmes du point de vue de leur groupe de symétrie.
I-2 Groupes : Introduction
Donnons la définition générale d'un groupe :
I-2-3 Exemple : les matrices d'ordre 2
Un exemple important pour la géométrie (et pour la physique) sont les groupes de symétrie ou groupes d'isométries.
I-2-4 Groupe de symétrie : un premier contact
I-2-1 Exemples de groupes
Commençons par des exemples arithmétiques ou numériques : relatifs, réels ou rationnels :
- ;
- ;
- ;
- il existe un élément tel que .
- ;
- ;
- ;
- .
- ;
- ;
- ;
- il existe un élément tel que .
Exercice
Exercice
Sous-groupe de racines de l'unité
Sous-groupe de racines de l'unité II
Sous-groupe de racines de l'unité III
Des manipulations sur trois boules permettent aussi de trouver un groupe :
(Lire la BD de Stewart : Ah les beaux groupes - les chroniques de Rose Polymath (Belin))
On a trois boules alignées. On peut ne pas changer leur ordre. C'est l'opération identité . On peut changer leur ordre en échangant les deux premières (opération ), en faisant tourner les trois dernières (opération ) et en effectuant ces opérations successivement. Donner le résultat comme un tableau : si une opération nouvelle apparaît, lui donner un nom ( , ...) et la rajouter.
| ... | |||||||||
| ... | |||||||||
On note la permutation qui transforme 1, 2, 3 en , , . Par exemple, est la permutation qui transforme 1, 2, 3 en 2, 3, 1.
Exercice
Permutations II
Permutations III
Enfin, voici un exemple de groupe formé d'applications.
I-2-2 Groupes : définition
Définition
-
loi interne
-
associativité
;
-
élément neutre
il existe un élément tel que ;
-
inverse
il existe un élément tel que .
L'ensemble muni de la loi est appelé un groupe.
Définition
Si a un nombre fini d'éléments, on représente la loi sous la forme d'un tableau.
Exercice
+ | pair | impair |
| pair | ||
| impair |
 | pair | impair |
| pair | ||
| impair |
Exercice
I-2-3 Exemple : les matrices d'ordre 2
On définit des opérations sur l'ensemble des matrices d'ordre 2 à coefficients réels :
Addition :
Exercice
Multiplication :
Exercice
Exercice
Exercice
I-2-4 Groupe de symétrie : un premier contact
Définition
Quelques exemples dans le plan :
- l'identité ;
- les rotations ;
- les réflexions par rapport à une droite ;
- les symétries centrales par rapport à un point.
Exercice [Le rectangle]
Suite
- l'identité
- les réflexions par rapport à chacune des médiatrices des côtés , ;
On peut composer ces transformations. En obtient-on d'autres ?
|
| ||||
|
| A | B | C | D |
|
| ||||
On a ainsi défini une application du groupe de symétrie du rectangle dans le groupe des permutations des quatre sommets , , et .
Exercice [Le triangle équilatéral]
Suite
- l'identité
- les réflexions par rapport à chacune des médiatrices , , ;
- les rotations d'angle , , et de centre .
On peut composer ces transformations. En obtient-on d'autres ?
|
| ||||||
|
| ||||||
L'ensemble est un groupe. On peut faire quelques remarques sur le tableau une fois rempli : que remarquez-vous sur chaque ligne ou sur chaque colonne ?
Comment chacune des ces transformations permutent-elles les sommets , , ?
|
| A | B | C |
|
| |||
Exercice [Autres figures]
I-2-5 Groupe de symétrie : définition
Définition
Exercice
Exercice
A | B | C | D | E | F | G | H | I | J | K | L | M |
N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
I-3 Rappels : Le plan complexe
- Un nombre complexe s'écrit où et sont des réels : est la partie réelle de , est la partie imaginaire de .
- Le conjugué de est .
- Le module de est .
- Tout nombre complexe de module 1 s'écrit
avec
unique modulo
: c'est
l'argument de
(on peut par exemple prendre
 entre 0 et
). On pose
.
entre 0 et
). On pose
.
- Tout nombre complexe
non nul s'écrit de manière unique
avec
et
 l'argument de
.
On représente un point du plan par son affixe :
l'argument de
.
On représente un point du plan par son affixe :
I-3-1 Quelques similitudes
I-3-2 Exercices
Exercice
Exercice
Exercice
Une similitude conserve les rapports de distance : il existe une constante telle que
Exercice
Exercice
- Triangle équilatéral
- Tir de rotation
- Billard circulaire (1 rebond)
- Billard circulaire (2 rebonds)
- Billard elliptique
- Triangles, rectangles et similitudes
- Composition de similitudes
- Figures et similitudes
-
Nature des transformations z -> az+b
Exercice
I-3-3 Indication pour trouver la nature géométrique
Pour trouver la nature géométrique d'une application du plan complexe de la forme
- Si , : il s'agit d'une translation de vecteur représenté par .
- Si
, l'équation
en
a une solution
et la transformation
a donc un
point fixe
d'affixe
. On peut alors écrire
- Si est réel, est une homothétie de rapport et de centre .
- Si
est un nombre complexe de module 1 et d'argument
 modulo
,
est une rotation
d'angle
modulo
,
est une rotation
d'angle
 et de centre
.
et de centre
.
- Si
est un complexe de module
et d'argument
 modulo
,
est une similitude
d'angle
modulo
,
est une similitude
d'angle
 , de centre
et de rapport
. Dans ce cas,
est le composé d'une homothétie
et d'une rotation.
, de centre
et de rapport
. Dans ce cas,
est le composé d'une homothétie
et d'une rotation.
II Géométrie du plan
Donnons d'abord quelques notions de base sur le plan vectoriel en s'appuyant sur le programme de terminale.
Voici quelques théorèmes dans le plan affine. Faites vous-même un dessin (et même plusieurs) pour comprendre l'énoncé de chacun de ces théorèmes.
Et le plan est plus riche si on introduit une structure euclidienne, c'est-à-dire une distance, une norme, un produit scalaire ... (d'ailleurs, dans le plan complexe, cela existe aussi).
II-1 Le plan vectoriel
II-1-1 Définitions et propriétés
II-1-1 Définitions et propriétés
Proposition
- (associativité) ;
- (élément neutre) ;
- (opposé) ;
- (commutativité) .
La multiplication d'un vecteur par un réel est compatible avec l'addition : pour tous vecteurs et du plan et tous réels et ,
- ;
- (distributivité) ;
- (distributivité) ;
- (élément absorbant) ;
II-1-2 Droites
Définition
Si , alors . On dit que est une équation de la droite . Si , on peut mettre cette équation sous la forme
II-1-3 Indépendance et colinéarité
Définition
Pour que deux vecteurs soient colinéaires, il faut et il suffit qu'ils appartiennent à la même droite.
Définition
Proposition
- et sont linéairement indépendants ;
- ;
- tout vecteur s'écrit de manière unique avec et dans .
II-1-4 Bases
Définition
Par exemple, les composantes de dans la base sont et .
Soient et les composantes de et dans la base . Alors, les composantes du vecteur dans la base sont , c'est-à-dire sous forme matricielle et en colonne :
Proposition
- Les vecteurs et sont colinéaires si et seulement si .
- L'ensemble des vecteurs dont les composantes dans la base vérifient est une droite vectorielle.
Exercice
Exercice
- A quelle condition sur le couple est-il une base du plan vectoriel ?
- Donner les coordonnées du vecteur dans la base en fonction des coordonnées dans la base usuelle.
Exercice
- Trouver l'intersection de 2 droites
- Trouver l'intersection de 2 droites II
- Trouver l'intersection de 2 droites II
- Fonctions linéaires/affines et droites
- Projections
- Tir aux vecteurs
II-2 Le plan affine
Le plan affine est toujours mais vu un peu différemment (on le note ici ). D'abord, on va appeler ses éléments des points. Un point du plan est donc encore un couple de réels. Le point a pour abscisse et pour ordonnée . On appelle bipoint un couple de points.
II-2-1 Translations
Définition
Remarquons qu'on vient de définir la notation où est un point et un vecteur.
Proposition
- est une bijection de dans ;
- ;
- .
Proposition
- Pour tout bipoint
, il existe un unique vecteur
tel que
.
On le note aussi
. On a donc la relation
- {Relation de Chasles} Pour tous points
,
,
de
, on a la relation
- Pour tout point du plan et tout vecteur , il existe un unique point tel que .
La troisième affirmation est la bijectivité de la translation .
II-2-2 Repères du plan
Définition
Exemple
Exercice
II-2-3 Droites affines
Définition
- ;
- est le translaté par le vecteur d'une droite vectorielle de base ; la droite est appelée direction de . La direction de est aussi l'ensemble des vecteurs pour et des points de . Un vecteur directeur de est une base de la direction de .
Définition
L'ensemble des points alignés avec deux points distincts du plan forme une droite. C'est la droite passant par ces deux points. Toute droite affine est aussi l'ensemble des points vérifiant une équation . Sa direction est d'équation .
Remarque
- se donner un point et un vecteur non nul ;
- se donner deux points distincts et ;
- écrire l'ensemble des points de la droite comme les points
tels que
soit colinéaire
à
pour un point
et un vecteur
non nul :
- écrire l'ensemble des points de la droite comme les points
barycentres de deux points
et
distincts :
- écrire l'ensemble des coordonnées des points de la droite :
- donner une relation entre les coordonnées
vérifiées par les coordonnées des points de
la droite et uniquement par eux.
Les vecteurs
et
sont des vecteurs directeurs. Le coefficient directeur (pente)
de la droite affine
est la pente de sa direction. C'est donc
si
avec
non nul et
 si
.
si
.
Exercice
II-2-4 Incidence
Définition
Proposition
- Pour que deux droites et soient parallèles, il faut et il suffit qu'il existe une translation telle que .
- Si est une droite affine et un point du plan, il existe une unique droite affine parallèle à et passant par (c'est-à-dire telle que ) : est l'image de la direction de par la translation de vecteur . Si est un point de , c'est aussi l'image de par la translation de vecteur .
Définition
Proposition
Proposition
Corollaire
Exercice
- Parmi les points suivants, lesquels sont alignés ?
,
,
,
,
- Déterminer l'intersection de et de .
Exercice
- Parmi les droites suivantes, déterminer lesquelles
sont parallèles, lesquelles sont concourantes et leurs points
d'intersection :
, , , ,
- Donner l'équation générale des droites passant par
.
- Déterminer l'équation de la parallèle
à
passant par
.
Exercice
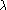 un réel non nul.
un réel non nul.- Donner l'équation de la droite
passant par les
points
et
.
- Soit
un point du plan. Donner tous les
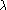 tels que
appartient à
.
tels que
appartient à
.
- Décrire
.
Exercice
- Donner les coordonnées des points et dans le repère .
- Donner une équation dans le repère usuel de la droite
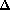 d'équation
dans le repère
.
d'équation
dans le repère
.
Exercice
II-2-5 Barycentres de points
Définition
Le milieu du segment est l'unique point tel que . Les coordonnées de , et vérifient
Proposition
Exercice
Proposition [Associativité du barycentre]
Quand les poids , ..., sont tous égaux, on appelle le barycentre l'isobarycentre ou centre de gravité.
Exemple [ Barycentre de deux points ]
Exercice
II-2-6 Polygones
Définition
Définition
Pour qu'un quadruplet (quadrilatère) soit un parallèlogramme, il faut et il suffit que les segments et aient même milieu.Définition
Définition
Proposition
II-2-7 Exercices
Exercice
Exercice
- Montrer que , , sont concourantes en .
- Montrer que
,
et
passent respectivement
par
,
et
.
Solution
- Montrons que est sur la droite . Par associativité du barycentre, est le barycentre de , , , et donc de , . Donc est sur la droite . De même pour les autres.
- Soit le barycentre de et . Alors, est le barycentre de et de , est le barycentre de et de . Donc , et sont alignés.
Exercice
Exercice
Exercice
- Barycentre de trois points
- Barycentre et côtés d'un triangle
- Barycentre : lequel ?
Exercice
- Tir de gravité I
- Tir de gravité II
- Tir de gravité III
- Coordonnées barycentriques
- Zones barycentriques
- Associativité du barycentre
II-3 Le plan affine avancé
II-3-1 Théorème de Thalès
Théorème [Thalès]
Proposition [Conséquence]
Il y a de nombreuses autres formulations du théorème de Thalès, par exemple :
Proposition
II-3-2 Théorème de Ceva
Théorème [Ceva]
Démonstration
Exemple
Exercice
Théorème [Médianes]
- Les médianes d'un triangle sont concourantes.
- Les médianes d'un triangle partagent celui-ci en six petits triangles d'aires égales.
- Les hauteurs d'un triangle sont concourantes.
II-3-3 Théorème de Ménélaüs
Théorème [Ménélaüs]
II-3-4 Birapport
Rappelons que si , sont deux points distincts, le rapport détermine la position d'un point de la droite par rapport à et .
Définition
Théorème
Démonstration
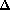 la droite sur laquelle se trouve les points
,
,
,
.
Soit
le projeté orthognal de
sur la droite
la droite sur laquelle se trouve les points
,
,
,
.
Soit
le projeté orthognal de
sur la droite
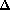 .
.
L'aire du triangle est égale à .
L'aire du triangle est égale à .
L'aire du triangle est égale à .
L'aire du triangle est égale à .
Ce qui montre facilement la première formule.
Pour la deuxième formule. on calcule l'aire des triangles précédents en choisissant une autre base :
Regardons maintenant le signe.
Le point est d'un côté de la droite ! On choisit une orientation pour tourner autour du point (le résultat ne dépend pas du choix car il y a 4 termes). Cela donne une orientation de la droite
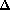 pour laquelle le sinus de
est positif si et seulement si
est positif pour deux points
et
de la droite
pour laquelle le sinus de
est positif si et seulement si
est positif pour deux points
et
de la droite
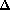 .
.
Corollaire
Soit un autre point, on a
Exercice
Conjugué harmonique
II-3-5 Théorème de Pappus
Théorème [Pappus]
Démonstration
Figure interactive (JSXGraph)
II-3-6 Théorème de Desargues
Théorème [Desargues]
Une autre formulation est :
Théorème
Ce fait est bien mis en évidence par l'applet suivante : Le point 1 (boule rouge) est l'intersection de trois droites concourantes de l'espace. Les triangles "homologues" sont les triangles 2, 3, 4 (boules violettes) et 5, 6, 7 (boules bleues). Les droites des côtés du triangle violet sont dans le plan de ce triangle et coupent les droites des côtés du triangle bleu selon l'intersection des deux plans qui est une droite (en général : oublions les cas de parallèlisme ...)
Mais pourquoi les droites des côtés homologues se coupent-elles ? Deux droites de l'espace ne se coupent pas en général (même si elles ne sont pas parallèles). Mais ici, ces droites sont dans un même plan : le plan contenant les deux droites concourantes au point rouge et portant respectivement un des deux sommets du côté et le sommet homologue. Et deux droites d'un plan sont sécantes ou parallèles.
conclusion
https://udascienza.unich.it/wims/wims.cgi?session=../tmp/robot.1&+cmd=getfile&+special_parm=file_74.spt, https://udascienza.unich.it/wims/wims.cgi?session=../tmp/robot.1&+cmd=getfile&+special_parm=file_74.xyz
II-3-7 Exercice : Droite de Newton
Exercice
Construction
Soient trois points , et non alignés.
II-3-8 Un autre exercice
Faire bouger les points de manière à les placer dans une situation non dégénérée. Que constatez-vous ? Conjecturer le sujet de l'exercice et le démontrer.
II-4 Le plan euclidien
Définition
II-4-1 Propriétés du produit scalaire
II-4-3 Version affine : la distance
II-4-1 Propriétés du produit scalaire
Proposition
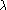 et
et
 des réels. Le produit scalaire vérifie les
propriétés suivantes :
des réels. Le produit scalaire vérifie les
propriétés suivantes :
Théorème [Théorème de Pythagore]
Théorème [Inégalité de Cauchy-Schwarz]
Proposition
II-4-2 Bases orthogonales
II-4-3 Version affine : la distance
Définition
Définition
Exercice
Exercice
Proposition
Définition
Si est d'équation , la droite vectorielle perpendiculaire à est d'équation .
Si et sont perpendiculaires et admettent respectivement comme équation et , alors .
Si a comme vecteur directeur , la droite vectorielle perpendiculaire à a comme vecteur directeur .
Proposition
II-4-4 Distance d'un point à une droite
Proposition
 perpendiculaire à
et passant par
. Soient
un point de
et
un vecteur de base de la direction
de
. Le point d'intersection
de
et de
perpendiculaire à
et passant par
. Soient
un point de
et
un vecteur de base de la direction
de
. Le point d'intersection
de
et de
 ,
appelé projeté orthogonal de
sur
vérifie :
,
appelé projeté orthogonal de
sur
vérifie :
Exercice
Proposition
On définit ainsi une application de dans qui à associe son projeté orthogonal sur . On l'appelle projection orthogonale sur .
Exercice
- Droite orthogonale
- Distance I
- Distance II
- Distance III
- Distance IV
- Projection I
- Projection II
II-4-5 Triangles
Définition
Théorème [Pythagore]
Définition
Proposition
Exercice
Exercice
- Montrer que la somme des distances de
aux côtés du triangle est égale à
.
- Soient , , les distances de à chacun des côtés , et respectivement. Montrer que est le barycentre de , ,
Solution
Exercice
II-4-6 Cercles
Définition
Définition
Proposition
Proposition
Proposition
Théorème [droite d'Euler]
II-4-7 Angles
 modulo
tel que
modulo
tel que
 est un nombre réel unique modulo
, c'est-à-dire unique à
l'addition près de
avec
un
entier relatif. On dit que
est un nombre réel unique modulo
, c'est-à-dire unique à
l'addition près de
avec
un
entier relatif. On dit que
 est un argument de
.
est un argument de
.Théorème [Al-Kachi]
Proposition
 un angle non nul.
un angle non nul.
- L'ensemble des points du plan tels que l'angle soit égal à est un cercle passant par et privé de et .
- Soient un cercle
de centre
et
,
et
trois points du cercle. Alors,
III Isométries du plan
Définition
III-2 Le groupe des isométries
III-1 Des exemples
Exercice
III-1-1 Les translations
En particulier,
III-1-2 Les rotations
Soient un point du plan et
 un réel.
un réel.Définition
 l'application qui à un point
associe le point
tel que
et tel que l'angle orienté
est égal à
l'application qui à un point
associe le point
tel que
et tel que l'angle orienté
est égal à
 modulo
; l'image de
est
lui-même.
modulo
; l'image de
est
lui-même.
Exercice
Exercice
 .
.- Le point
est fixe et c'est le seul point fixe par
si l'angle de la rotation est non nul.
DémonstrationPar définition, donc . D'autre part, si est un autre point fixe,Donc l'angle de la rotation est nul.
-
est une isométrie et
.
DémonstrationOn desine et on regarde les triangles et . Les côtés et d'une part et et d'autre part sont égaux par définition de . On a alors l'égalité d'anglesDonc
Les deux triangles et ont deux côtés égaux et un angle égal, ils sont donc égaux. Donc les troisièmes côtés sont égaux :Ce qui prouve que est une isométrie. Les deux autres angles sont aussi égaux :
- la rotation respecte les angles et l'orientation
Démonstration
Proposition
Démonstration
-
Le composé de deux rotations de centre
Le composé de deux rotations et de centre et d'angles respectifs et est une rotation de centre et d'angle : en effet,en prenant , on obtientPour les angles,
-
L'inverse d'une rotation
L'inverse de la rotation de centre et d'angle
 est la rotation de centre
et d'angle
.
est la rotation de centre
et d'angle
.
-
Le composé d'une rotation et d'une translation
Étudions le composé d'une translation et d'une rotation . Construisons un point fixe géométriquement. Notons-le .
Le composé de deux isométries est une isométrie, donc on a bien la relationOn a d'autre part
Proposition
Démonstration
Exercice
Quel est le centre de rotation de , de ? Comment le construire géométriquement ?
Remarque
Prenons d'abord pour l'origine . Si et , on obtient
On vérifie ainsi que la rotation de centre et d'angle
 est une application linéaire.
est une application linéaire.Pour quelconque, on a les formules
Le déterminant de la matrice est égal à .
III-1-3 Les réflexions
Définition
Proposition
 perpendiculaires à
sont globalement invariantes par
:
.
Une réflexion
transforme les angles en leur opposé :
perpendiculaires à
sont globalement invariantes par
:
.
Une réflexion
transforme les angles en leur opposé :
Exercice
Remarque
Soit
 l'angle que fait le vecteur
avec le vecteur
. On a donc
,
et on peut prendre
.
Alors la matrice de
dans le repère
est
l'angle que fait le vecteur
avec le vecteur
. On a donc
,
et on peut prendre
.
Alors la matrice de
dans le repère
est
Cela peut se voir géométriquement~. Si est l'image de par la réflexion , comme l'angle de porté par avec est
 , l'angle
que fait
avec son image est
.
, l'angle
que fait
avec son image est
.
Le déterminant de est .
Exercice
III-1-4 Les symétries glissées
Que donne le composé d'une réflexion et d'une translation ?
Définition
On a
Proposition
- Si
est perpendiculaire à
,
est une réflexion par rapport à la droite translatée de
par le vecteur
- Si
n'est pas perpendiculaire à
, posons
avec
la projection de
sur
et
perpendiculaire à
et
soit
la droite translatée de
par le vecteur
.
Alors,
est la symétrie
glissée d'axe de glissage
et de vecteur
.
Exercice
Exemple
III-2 Le groupe des isométries
III-2-1 Structure de groupe
Proposition
- le produit (composé) de deux isométries est une isométrie ;
- une isométrie est une bijection de dans , elle admet une application réciproque qui est aussi une isométrie.
Rappel
La chose délicate à montrer est qu'une isométrie est bijective. Nous pourrons déduire ce fait de considérations d'algèbre linéaire. Mais nous allons ici le faire de manière géométrique.
Démonstration
Remarque
Proposition
Proposition
III-2-2 Les isométries positives
Proposition
Démonstration
Soit un point d'image distincte de et la rotation de centre envoyant sur . Alors laisse fixe et et préserve l'orientation.
Si n'est pas l'identité, prenons un point non fixe par . Comme et sont à égale distance de et de , la droite est la médiatrice de et . Donc coïncide avec la réflexion par rapport à la droite sur trois points, elle lui est donc égale. Comme conserve l'orientation, ce n'est pas possible. Donc, est l'identité et est une rotation.
Le composé de deux rotations est une rotation ou une translation.
Démonstration
III-2-3 Liste des isométries du plan
Proposition
- translation par un vecteur ;
- rotation d'angle
 de centre un point
;
de centre un point
;
- réflexion par rapport à une droite ;
- symétrie glissée obtenue en faisant une réflexion par rapport à une droite , puis en translatant par un vecteur non nul parallèle à .
Démonstration
- est une réflexion.
-
est le composé de deux réflexions par rapport à deux droites
et
.
Alors,
respecte l'orientation.
-
Les droites et sont parallèles
Alors est une translation.
-
les droites et ne sont pas parallèles
Le point d'intersection de et est fixe par : . Soit un point tel que est différent de . Soit la rotation de centre et envoyant sur . Alors a deux points fixes et .
Supposons que ne soit pas l'identité : soit un point différent de . Alors, est la médiatrice de . Soit la réflexion par rapport à la droite . Alors, est une isométrie laissant fixe trois points. C'est donc l'identité. Mais comme est une isométrie positive et une isométrie négative, ce n'est pas possible. Donc, est l'identité et est une rotation.
-
Les droites et sont parallèles
-
est le composé de trois réflexions
par rapport à trois droites
,
et
.
En particulier,
ne conserve pas l'orientation.
-
Les droites , et sont parallèles
L'isométrie est une translation de vecteur perpendiculaire à la direction des trois droites. Le composé avec est encore une réflexion par rapport à la droite translaté de
-
Les droites , sont parallèles
L'isométrie est une translation de vecteur perpendiculaire à la direction des deux droites et . Le composé avec est une réflexion glissée d'axe de glissage la droite translatée de par où est le projeté du vecteur sur une perpendiculaire à .
-
Les droites , sont parallèles
On traite ce cas comme le précédent.
-
Les droites , sont parallèles
Idem.
-
Les droites , et sont concourantes
Soit le point d'intersection de , et . Le composé est une rotation de centre que l'on peut écrire comme avec une droite convenable : plus précisément est la droite passant par dont l'angle avec est égal à l'angle de avec . On a alorsDonc, est une réflexion.
L'axe de symétrie passe par et est la droite des milieux . Pendre par exemple pour un point de .
-
Les droites , et ne sont pas concourantes
Le composé est une rotation de centre le point d'intersection de et et d'angle non nul. On peut l'écrire comme avec la droite parallèle à passant par et une droite convenable : plus précisément est la droite passant par dont l'angle avec est égal à l'angle de avec . On a alorsoù est un vecteur perpendiculaire à . Ce vecteur n'est pas perpendiculaire à car n'est pas parallèle à . Donc, est une réflexion glissée.
L'axe de glissage passe la projection de sur et par la projection de sur . En effet, l'image de par est son symétrique par rapport à la droite et l'axe de glissage passe par le milieu de . L'image par du symétrique de par rapport à est .
-
Les droites , et sont parallèles
Remarque
III-2-4 Exercices
Exercice
Exercice
Exercice
Exercice
Exercice
Exercice
Exercice
Exercice
Exercice
Exercice
Exercice
Exercice
III-3 Point de vue de l'algèbre linéaire
III-3-1 Matrices orthogonales
Si est une matrice, la matrice transposée est par définition la matrice obtenue en échangeant les lignes et les colonnes :
Les matrices des rotations et des réflexions vérifient .
Définition
Proposition
Proposition
- est orthogonale ;
- les colonnes de sont des vecteurs unitaires (deux à deux) orthogonaux ;
- l'application linéaire
de matrice
dans la base
vérifie
Proposition
Proposition
III-3-2 Isométries
Proposition
- est une isométrie fixant l'origine ;
-
préserve le produit scalaire :
-
est la multiplication à gauche par une matrice orthogonale :
si
et
, alors
avec (application linéaire orthogonale).
III-4 Composé et transformé
On peut composer deux isométries mais il y a une opération plus naturelle : transformer une isométrie par une autre.
Définition
- transformée par de la translation de vecteur la translation de vecteur .
- transformée par
de la rotation de centre
et d'angle
 la rotation de centre
et d'angle
la rotation de centre
et d'angle
 ;
;
- transformée par de la réflexion orthogonale d'axe la réflexion orthogonale d'axe ;
On note la transformée de par . On parle aussi de conjuguée. Cette opération est beaucoup plus simple que la composée ! Il suffit de transformer les invariants.
Dans , on peut quand même interpréter la transformée comme un composé :
Proposition
- Soient
une translation de vecteur
et
la rotation de centre
et d'angle
 .
Soit
l'image de
par
. Alors
autrement dit .
.
Soit
l'image de
par
. Alors
autrement dit . - Soient
la translation de vecteur
et
la réflexion par rapport à
. Soit
l'image de
par la translation
. Alors autrement dit, .
- On note
la réflexion orthogonale par rapport à la droite
,
la translation
de vecteur
,
la symétrie centrale par rapport à un point
du plan.
- si
est parallèle à
, autrement dit
- si
est perpendiculaire à
,
autrement dit
- autrement dit
- si
est parallèle à
,
On peut utiliser le fait que le carré d'une réflexion est l'identité pour simplifier les formules.
III-5 Formulaires
Exercice
- ;
- si et sont deux droites parallèles, avec , et perpendiculaire aux deux droites ;
- Si
,
où
 est la droite perpendiculaire à
passant par
;
est la droite perpendiculaire à
passant par
;
- Si
,
où
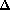 est la droite perpendiculaire à
passant par
,
et
la projection orthogonale de
sur
.
est la droite perpendiculaire à
passant par
,
et
la projection orthogonale de
sur
.
- Si
et
sont des droites affines passant par un point
et
 l'angle
orienté de
et de
,
l'angle
orienté de
et de
,
Exercice
Exercice
- Si
est une translation, on prend pour
l'identité
et pour translation la translation
.
- Si
est une rotation de centre
, on prend pour
la rotation
de centre
et pour translation la translation de vecteur
.
Exemple
- Si
est une réflexion d'axe
, on prend la droite
parallèle à
et
passant par
,
la réflexion d'axe
et pour translation la
translation de vecteur
où
est le
vecteur perpendiculaire aux droites
et
avec
sur
.
Exemple
- Si
est une réflexion glissée d'axe
et de vecteur
(parallèle
à
),
on prend la droite
parallèle à
et
passant par
,
la réflexion d'axe
et pour translation la
translation de vecteur
où
est
le vecteur perpendiculaire aux droites
et
avec
sur
.
III-6 Exercices
Exercice
Exercice
Exercice
- Soit
et
la rotation de centre
et
d'angle
. On écrit
comme le composé
d'une translation de vecteur
et d'une rotation de centre
.
Quel est l'angle de la rotation
? Calculer le vecteur
.
Faire de même en écrivant
.
- Faire de même avec la rotation de centre
et de d'angle
:
- Qu'obtient-on pour
?
- Écrire la rotation précédente comme composé de deux réflexions.
IV Groupes et groupes d'isométrie
Nous avons des groupes concrets à notre disposition, nous allons revenir aux groupes d'isométries du plan, autrement dit les groupes de symétrie d'un système. Dans ce paragraphe, nous n'étudierons de tels groupes que lorsqu'ils sont finis.
Les groupes que nous venons de rencontrer sont
- le groupe des isométries de laissant fixe (dans sa version vectorielle, le groupe des isométries de laissant fixe ) ;
- le groupe des rotations de laissant fixe , ou ce qui revient au même le groupe des isométries positives de laissant fixe ;
- le groupe des isométries ;
- le groupe des isométries positives de (rotation-translation) ;
- le groupe linéaire (le groupe des applications linéaires bijectives de ) ;
- le groupe affine des composés de translations et d'applications linéaires (laissant fixe ).
IV-1 Groupes d'isométries ou de symétrie
Nous n'avons pour l'instant donné que la définition d'un groupe. Il est temps d'en faire un peu plus :
Un groupe de symétrie qui est fini fixe toujours un point du plan et on peut complétement déterminer sa structure. C'est ce qu'on va faire dans le paragraphe suivant.
IV-7 Les groupes d'isométries du plan qui sont finis
Un groupe d'isométries qui n'est pas fini n'a pas toujours de points fixes : prenons par exemple le groupe des isométries d'une droite du plan. Pour l'étudier, on introduit la notion de groupe ponctuel (ou groupe vectoriel).
IV-1 Groupes d'isométries ou de symétrie
Définition
Remarque
Exercice
Exercice
Si est fini, numérotons ses points ou même 1, ..., . Soit un élément de . On peut alors définir la permutation des points de
On a ainsi une action de sur l'ensemble .
Définition
- pour ;
- pour , , .
Exemple
-
opère sur
.
- Le groupe du carré opère sur l'ensemble
des sommets d'un carré.
- Le groupe du carré opère aussi sur l'ensemble des côtés du carré.
- Le groupe du carré opère sur l'ensemble des couples formés d'un côté et d'un de ses sommets. Combien d'éléments l'ensemble a-t-il ?
IV-2 Sous-groupes et ordre
Définition
- si et appartiennent à , appartient à ;
- l'élément neutre de appartient à ;
- si appartient à , appartient à .
Exercice
- L'ensemble des matrices de la forme avec est un sous-groupe de .
- L'ensemble des matrices de la forme avec et est un sous-groupe de .
Définition
 sinon.
sinon.
Exercice
- Soient et deux réflexions d'axe et . Quel est l'ordre de et ? de leur composé ?
- Soit
une rotation d'angle
et
une translation. Calculer l'ordre
de
.
- Calculer l'ordre de , de , de .
Proposition
IV-3 Sous-groupe engendré
Définition
Exercice
Exercice
Exercice
Exercice
IV-4 Groupe cyclique
Définition
Exemple
IV-5 Morphismes de groupes
Définition
Un isomorphisme de groupes est un homomorphisme de groupes qui est bijectif. On dit alors que les groupes et sont isomorphes.
Exercice
Exemple
Exercice
IV-6 Sous-groupes invariants
Définition
Exemple
- Le sous-groupe des rotations est un sous-groupe distingué du groupe , puisque le transformé d'une rotation de centre par une isométrie laissant fixe est encore une rotation de centre .
- Par contre le transformé d'une rotation de centre par une translation par un vecteur non nul n'est pas une rotation de centre . Donc n'est pas distingué dans .
Exercice
Exercice
Trouver le sous-groupe de symétrie de figures
IV-7 Les groupes d'isométries du plan qui sont finis
Proposition
Démonstration
- On prend un point
dans le plan et on construit les images de
par
tous les éléments de
. Comme
est fini formé de
isométries
, ...,
,
on obtient ainsi
points
Soit l'isobarycentre de , ..., .
- Appliquons à
n'importe
lequel des éléments
de
. Alors, l'ensemble des
est l'ensemble
des éléments de
qui se trouvent sur la ligne correspondant à
dans le tableau de la
loi,
c'est donc en fait exactement tous les
mais dans un ordre différent.
Donc l'isobarycentre des
est l'isobarycentre des
c'est-à-dire
.
-
Il reste à voir que l'image par
de
est aussi l'isobarycentre des
.
Toute isométrie est le composé d'une translation et d'une isométrie
laissant fixe un point. On vérifie que cela est vrai pour deux telles isométries et
donc pour leur composé.
- Donc .
Théorème
- le sous-groupe de
engendré par la rotation de centre
et d'angle
;
- le sous-groupe de engendré par la rotation de centre et d'angle et une réflexion axiale d'axe passant par .
Corollaire
- soit le sous-groupe de engendré par la rotation de centre et d'angle ,
- soit le sous-groupe de engendré par la rotation de centre et d'angle et une réflexion axiale d'axe passant par (on l'appelle groupe diédral).
IV-8 Exercices
Exercice
Exercice
Exercice
Calcul dans le groupe diédral
Trouver le groupe de symétrie de figures
Exercice
Exercice
IV-9 Coloriages
IV-9-3 Stabilisateur d'une couleur
IV-9-1 Que colorier
On trouve triangles. Le groupe de symétrie de est d'ordre . Le stabilisateur d'un sommet, c'est-à-dire le sous-groupe des isométries qui stabilisent (laissent fixe) ce sommet, est formé de l'identité et de la symétrie par rapport à la droite passant par ce sommet et par le centre de .
On peut aussi vouloir colorier les couples formés d'un sommet et d'un côté qui le contient. On obtient alors triangles.
Exercice
On dit que agit transitivement sur l'ensemble des sommets (ou l'ensemble des côtés).
IV-9-2 Comment colorier
Définition
- formant une partition : la réunion des est et les ensembles sont disjoints deux à deux : ;
- tel que pour tout et pour tout , est un des de la famille.
Voici des exemples de bons coloriages (compatibles au groupe d'isométries du polygone).
IV-9-3 Stabilisateur d'une couleur
On a la propriété suivante
Proposition
Démonstration
En particulier, si , c'est-à-dire si est dans le stabilisateur de , est dans le stabilisateur de la couleur de :
Choisissons une couleur et soit son stabilisateur. Les autres couleurs sont de la forme pour un certain et le stabilisateur de est
IV-9-4 Comment construire les coloriages
Nous allons donner une méthode de construction de coloriages de pour l'ensemble des sommets, ou des côtés, ou des couples sommets/côtés, en partant d'un sous-groupe de .
- Choisissons un élément
de
et un sous-groupe
de
. D'après ce qu'on vient d'étudier, pour que
puisse être le stabilisateur de la couleur
de
, il est nécessaire que
contienne le stabilisateur de
(qui est le sous-groupe engendré par une réflexion dans le cas des sommets ou des côtés et le groupe trivial
dans le cas des sommets/côtés). On le suppose donc.
-
Soit
. Vérifions que les
pour
vérifient la propriété
des coloriages. Notons les ensembles distincts
pour
.
Comme
agit transitivement sur
, la réunion des
est tout
. Il reste à montrer que si
est non vide, alors
.
Soit
un élément de
,
on a donc en écrivant tout ce qu'on sait,
avec et appartenant à . D'oùce qui implique que appartient au stabilisateur de , donc à . Donc, et
- Ainsi, les sous-ensembles pour forment bien un coloriage de .
IV-9-5 Exercices
Exercice
Exercice
Exercice
- On considère un polygone régulier à 9 côtés. Décrire son groupe de symétrie (nom, nombre d'éléments, générateurs, ...)
- On trace les triangles dont un sommet est au centre du polygone et tel que le côté opposé à ce sommet soit un demi-côté (allant d'un sommet au milieu des côtés dont il est l'extrémité). Combien y a-t-il de tels triangles ?
- Soit une rotation d'angle et le sous-groupe qu'il engendre dans . Dessiner un coloriage de ces triangles construit associé à . Combien de couleurs faut-il ? Dessiner tous les coloriages à deux ou trois couleurs compatibles avec et donner le stabilisateur d'une des couleurs dans chaque cas.
IV-10 Groupe ponctuel
Proposition
- Comportement par composition : pour un vecteur .
- Soit un groupe d'isométries et soit l'ensemble des isométries laissant fixe obtenues de la manière précédente à partir des éléments de . Alors, est un groupe.
- Si
est un autre point de
et si
la translation de vecteur
(ainsi,
), on a
Exercice
Attention, il n'y a aucune raison que soit contenu dans . Un premier exemple de cette situation est le suivant : soit le groupe engendré par la rotation de centre et d'angle ; est engendré par la rotation de centre et d'angle . Mais cet exemple est un peu artificiel ...
Définition
Si l'on peut, on choisit l'origine de manière à simplifier les calculs. Modulo conjugaison, le groupe ponctuel qu'on note abusivement n'en dépend pas.
Par exemple, si est une figure dont le groupe d'isométrie est fini, le meilleur choix pour calculer son groupe ponctuel est bien sûr le centre de gravité de . Avec ce choix, .
Exercice
Groupe ponctuel d'une frise